ブログ

トンネル効果

この効果は電子が波動であることの立証になる。

エネルギー障壁の高さ$V_1$は十分に高くて、電子のエネルギーよりも大きいとする。電子を粒子とすると、電子のはこの障壁を越えることができず、境界ですべて反射されてしまう。とこらが電子を波動と考えると、この障壁中に浸み込んでいくことが可能になる。この効果をトンネル効果という。

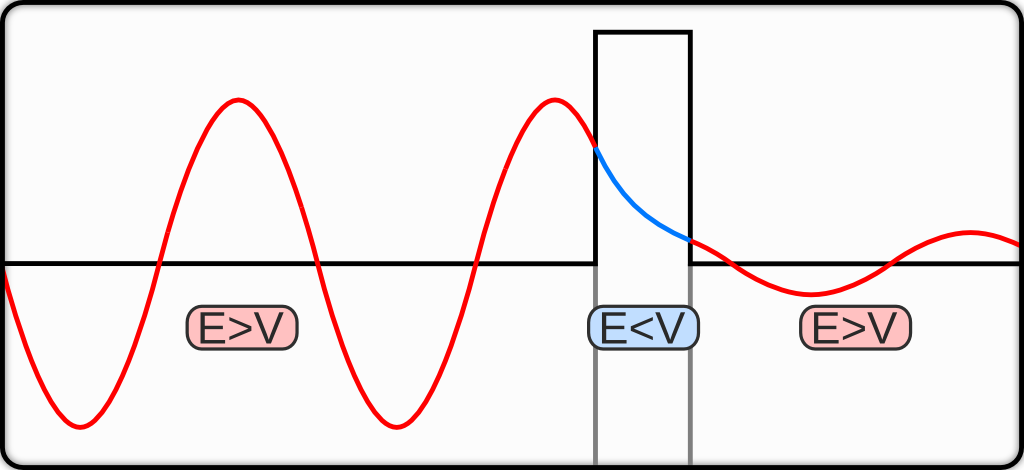
トンネル抜け前後で粒子のエネルギー（波長）は変わらないが確率振幅は減少する。

トンネル確率P

単位時間に単位面積を通過する入射波と透過波の電子数の比と定義する。

任意の形をとる時には

$$P\fallingdotseq A\cdot exp(-\frac{2}{\hslash }\sqrt{2m}{\int }_0^{x_1}\sqrt{|V(x)-E|}\cdot dx)$$

$E=V_1∕2$ をとる時には

$$P=4\cdot exp(-\frac{2m\sqrt{gh}}{\hslash }\cdot W)$$